Wednesday, 4 July 2007
Friday, 11 May 2007
P=NP

I was reading the arXiv 'headlines' today and found this. I am very skeptical about such breakthroughs once that the P=NP question is so important that it is one of the Millenium Prize problems.
For those who are not experts, I'll give a brief account of the problem. There are two main complexity classes of algorithms with respect to the time of computation: P and NP. The P class is the class of algorithms that give an answer in what is called polynomial time. This means that the time the algorithm takes to give you an answer is proportional to some power of the size of the question. This doesn't look so atractive if this power is very large, for example 20, but is always better than the NP class. The NP class is the class of algorithms which, although you can check if the solution is correct in polynomial time, if fed with a question they will take an exponential time with respect to the size of the question to give you an answer. If you remember your math classes, the exponential always grows faster than any polynomial. So, when the question gets big, it is really a problem.
The classical example, and the most important from the strategic/economic/etc point of view, is prime decomposition. Everybody knows that the public key cryptographic scheme is based on factoring an integer in two very large prime factors. This problem is NP, for the best algorithm known to solve the problem takes a time which is exponential in the size (the number of digits) of the number to be factorized. Note that I am not saying that there is no P algorithm which does that, only that it is not known. This is precisely the point: there is no proof that you cannot find a P algorithm to solve all problems. If you can, the cryptographic security of Internet is lost as codes could be broken very fast. There are fundamental issues that are also important, but I would say that security is one of the main concerns here...
Now, this guy claims that he found a P algorithm for every problem, whcih must include prime factorization. I will just point to the paper and wait for the revision of experts:
Does P=NP?
Karlen Garnik Gharibyan
arXiv:0705.1442v1 [cs.CC]
For those who are not experts, I'll give a brief account of the problem. There are two main complexity classes of algorithms with respect to the time of computation: P and NP. The P class is the class of algorithms that give an answer in what is called polynomial time. This means that the time the algorithm takes to give you an answer is proportional to some power of the size of the question. This doesn't look so atractive if this power is very large, for example 20, but is always better than the NP class. The NP class is the class of algorithms which, although you can check if the solution is correct in polynomial time, if fed with a question they will take an exponential time with respect to the size of the question to give you an answer. If you remember your math classes, the exponential always grows faster than any polynomial. So, when the question gets big, it is really a problem.
The classical example, and the most important from the strategic/economic/etc point of view, is prime decomposition. Everybody knows that the public key cryptographic scheme is based on factoring an integer in two very large prime factors. This problem is NP, for the best algorithm known to solve the problem takes a time which is exponential in the size (the number of digits) of the number to be factorized. Note that I am not saying that there is no P algorithm which does that, only that it is not known. This is precisely the point: there is no proof that you cannot find a P algorithm to solve all problems. If you can, the cryptographic security of Internet is lost as codes could be broken very fast. There are fundamental issues that are also important, but I would say that security is one of the main concerns here...
Now, this guy claims that he found a P algorithm for every problem, whcih must include prime factorization. I will just point to the paper and wait for the revision of experts:
Does P=NP?
Karlen Garnik Gharibyan
arXiv:0705.1442v1 [cs.CC]
Wednesday, 25 April 2007
Blogophysics

I was reading the files on arXiv this week and found the paper:
Cascading Behavior in Large Blog Graphs
Jure Leskovec, Mary McGlohon, Christos Faloutsos, Natalie Glance, Matthew Hurst
arXiv:0704.2803v1 [physics.soc-ph]
I remember that I have already seen a paper about blogs before and I am almost sure that Osame wrote about that in his blog, so I made a little search on arXiv and found these ones, in reverse chronological order:
Social Information Processing in Social News Aggregation
Kristina Lerman
arXiv:cs/0703087v2 [cs.CY]
Information propagation and collective consensus in blogosphere: a game-theoretical approach
Lianghuan Liu, Feng Fu, Long Wang
arXiv:physics/0701316v1 [physics.soc-ph]
Social Networks and Social Information Filtering on Digg
Kristina Lerman
arXiv:cs/0612046v1 [cs.HC]
Social Browsing on Flickr
Kristina Lerman, Laurie Jones
arXiv:cs/0612047v1 [cs.HC]
The structure of self-organized blogosphere
Feng Fu, Lianghuan Liu, Kai Yang, Long Wang
arXiv:math/0607361v3 [math.ST]
Quantitive and sociological analysis of blog networks
Wiktor Bachnik, Stanislaw Szymczyk, Piotr Leszczynski, Rafal Podsiadlo, Ewa Rymszewicz, Lukasz Kurylo, Danuta Makowiec, Beata Bykowska
arXiv:physics/0506051v1 [physics.soc-ph]
It seems that Kristina Lerman, a physicist who became a computer scientist, is the most active in this area. Take a look at her homepage.
Basically, blogs are considered as vertices of a graph and links between blogs as its edges. Well, this kind of network has been studied in physics for some time now. There are a lot of things you can study, but I will highlight just the most common one. Usually, what is studied is the distribution of edges in the graph, i.e., the number of vertices with 1,2,3,... edges. The interesting result, which appears in a lot of different networks in nature, from the famous small world networks to chemical networks in the cells, is that this distribution obeys what is called a power-law:

where r is the number of edges and k is a constant. This kind of formula is important in physics, because it indicates that the characteristics of the distribution do not change when the scale of the problem changes, i.e., if we analyse 10, 100, 1000, 10000 blogs, the distribution will be the same (dicarding finite size effects). We call this distributions scale-free. To have a feeling of the importance of these power-laws, they appear in second-order phase transitions and in self-organised criticality (which is not unrelated).
All this again falls in the huge multidisciplinary range of complex systems, which is highly fashionable (specially if you want to ask for a research grant) but difficult to define. Although we could say that complex systems are systems composed by a large number of interacting units which can manifest some kind of emergent behaviour, maybe it would be simpler to say that complex systems are all those which are not simple.
In the beginning of this blog, I wrote a post about avalanches. This is considered a complex system with emergent behaviour: the avalanches. The real ones don't, but simplified ones in computer models have a distribution of sizes which is a power-law. These relationships are still not well understood, but they indicate connections between a lot of phenomena and we hope this will be clarified during this century (well, at least I hope...).
Picture: from Data Mining. The original caption is:
This graph shows another view of the core. Rather than require reciprocal links, I have simply pulled out the largest connected component formed by any directional link between blogs. The obvious insight here is the relationship between LiveJournal (blue) and the rest of the core.
Cascading Behavior in Large Blog Graphs
Jure Leskovec, Mary McGlohon, Christos Faloutsos, Natalie Glance, Matthew Hurst
arXiv:0704.2803v1 [physics.soc-ph]
I remember that I have already seen a paper about blogs before and I am almost sure that Osame wrote about that in his blog, so I made a little search on arXiv and found these ones, in reverse chronological order:
Social Information Processing in Social News Aggregation
Kristina Lerman
arXiv:cs/0703087v2 [cs.CY]
Information propagation and collective consensus in blogosphere: a game-theoretical approach
Lianghuan Liu, Feng Fu, Long Wang
arXiv:physics/0701316v1 [physics.soc-ph]
Social Networks and Social Information Filtering on Digg
Kristina Lerman
arXiv:cs/0612046v1 [cs.HC]
Social Browsing on Flickr
Kristina Lerman, Laurie Jones
arXiv:cs/0612047v1 [cs.HC]
The structure of self-organized blogosphere
Feng Fu, Lianghuan Liu, Kai Yang, Long Wang
arXiv:math/0607361v3 [math.ST]
Quantitive and sociological analysis of blog networks
Wiktor Bachnik, Stanislaw Szymczyk, Piotr Leszczynski, Rafal Podsiadlo, Ewa Rymszewicz, Lukasz Kurylo, Danuta Makowiec, Beata Bykowska
arXiv:physics/0506051v1 [physics.soc-ph]
It seems that Kristina Lerman, a physicist who became a computer scientist, is the most active in this area. Take a look at her homepage.
Basically, blogs are considered as vertices of a graph and links between blogs as its edges. Well, this kind of network has been studied in physics for some time now. There are a lot of things you can study, but I will highlight just the most common one. Usually, what is studied is the distribution of edges in the graph, i.e., the number of vertices with 1,2,3,... edges. The interesting result, which appears in a lot of different networks in nature, from the famous small world networks to chemical networks in the cells, is that this distribution obeys what is called a power-law:
where r is the number of edges and k is a constant. This kind of formula is important in physics, because it indicates that the characteristics of the distribution do not change when the scale of the problem changes, i.e., if we analyse 10, 100, 1000, 10000 blogs, the distribution will be the same (dicarding finite size effects). We call this distributions scale-free. To have a feeling of the importance of these power-laws, they appear in second-order phase transitions and in self-organised criticality (which is not unrelated).
All this again falls in the huge multidisciplinary range of complex systems, which is highly fashionable (specially if you want to ask for a research grant) but difficult to define. Although we could say that complex systems are systems composed by a large number of interacting units which can manifest some kind of emergent behaviour, maybe it would be simpler to say that complex systems are all those which are not simple.
In the beginning of this blog, I wrote a post about avalanches. This is considered a complex system with emergent behaviour: the avalanches. The real ones don't, but simplified ones in computer models have a distribution of sizes which is a power-law. These relationships are still not well understood, but they indicate connections between a lot of phenomena and we hope this will be clarified during this century (well, at least I hope...).
Picture: from Data Mining. The original caption is:
This graph shows another view of the core. Rather than require reciprocal links, I have simply pulled out the largest connected component formed by any directional link between blogs. The obvious insight here is the relationship between LiveJournal (blue) and the rest of the core.
Friday, 13 April 2007
Wednesday, 4 April 2007
300 and Science Fiction

Last Saturday I saw '300' in the cinema. I must say I really enjoyed the film. Usually, I don't bother with the critics about a movie, but I was curious since the actor that makes Xerxes is brazilian (Rodrigo Santoro) and well known in my country. I like to see brazilians doing well in the international scenario.
Appart from the usual critics to action movies and to the actors and the conspiracy theories about the political intentions of the film, there was one that I found very interesting. It was repeated by a lot of people: the fact that the movie is not historically accurate. The fact that they were not just observations, but that the critics were pointing this as a negative feature capable of lowering the quality of the work should be analysed better.
When I was younger, I used to tease my friends telling them what was scientifically wrong with the Sci-Fi movies. I liked the movies a lot, but I kept noticing every detail and criticizing them after leaving the cinema. I don't need to say that my friends didn't like it. Most of the time, except when they asked about it, they were not interested in how real or possible were the actions or devices in the film. Can you imagine why? Well, in the beginning I couldn't, so I started to think about paying attention in myself.
I realised that when I go to a movie, I am not interested in having a science class, I am interested in the emotions I feel. I liked Star Wars even with the sound of explosions in the empty space, with the vision of the laser beams and with millions of other small details. I like to see Star Trek (although the guys try very hard to justify everything). I liked Matrix even knowing that the machines could not use the humans in that way without violating energy conservation. I did like Sci-Fi movies independently of the scientific failures if the underlying plot is well written and the effects and the actors are good. I don't wanna know why, I just wanna leave the cinema feeling better (or in the case of dramas, worse) than I entered.
Indeed, I have never seen any critic saying that a Sci-Fi movie is bad because it does not pay attention to the laws of physics, have you? Maybe it is because it is easier to spot history failures than science failures. But when I was in the cinema this Saturday, I could see that everyone was holding their breaths and no one left the room to go to the toilette, as is so common. I left the cinema feeling very good.
I believe that Frank Miller's comic book was not intended to be historically accurate. I believe it was meant to be cool. I know that a lot of people will say that this is bad, because it makes people learn wrong history. Really? Well, in my case, it was pretty obvious that the film was a kind of fiction, unless you really believe that the Persian soldiers were inhuman monsters and that a Spartan soldier can put a spear in the eyes of a giant battle Rhino who is charging on him killing the beast just centimeters before it reaches the target. Of course it was not real! So, the first thing I did when I arrived home was to open a History book and learn what was really known about the fact. See? Although I have never been good in history on my school days, I was led to study it by seeing a movie that made me feel well. If I would have left the cinema feeling that I have thrown my money away, I would never have done that.
In fact, one of the things that led me to be a scientist (and I bet it is the same for many others!) was the Sci-Fi movies. I wanted to live that and, above all, to understand that. Indeed, I almost gave up to be a physicist and just came back after seeing Contact, but this is another story.
Picture: cover of the comic book.
Appart from the usual critics to action movies and to the actors and the conspiracy theories about the political intentions of the film, there was one that I found very interesting. It was repeated by a lot of people: the fact that the movie is not historically accurate. The fact that they were not just observations, but that the critics were pointing this as a negative feature capable of lowering the quality of the work should be analysed better.
When I was younger, I used to tease my friends telling them what was scientifically wrong with the Sci-Fi movies. I liked the movies a lot, but I kept noticing every detail and criticizing them after leaving the cinema. I don't need to say that my friends didn't like it. Most of the time, except when they asked about it, they were not interested in how real or possible were the actions or devices in the film. Can you imagine why? Well, in the beginning I couldn't, so I started to think about paying attention in myself.
I realised that when I go to a movie, I am not interested in having a science class, I am interested in the emotions I feel. I liked Star Wars even with the sound of explosions in the empty space, with the vision of the laser beams and with millions of other small details. I like to see Star Trek (although the guys try very hard to justify everything). I liked Matrix even knowing that the machines could not use the humans in that way without violating energy conservation. I did like Sci-Fi movies independently of the scientific failures if the underlying plot is well written and the effects and the actors are good. I don't wanna know why, I just wanna leave the cinema feeling better (or in the case of dramas, worse) than I entered.
Indeed, I have never seen any critic saying that a Sci-Fi movie is bad because it does not pay attention to the laws of physics, have you? Maybe it is because it is easier to spot history failures than science failures. But when I was in the cinema this Saturday, I could see that everyone was holding their breaths and no one left the room to go to the toilette, as is so common. I left the cinema feeling very good.
I believe that Frank Miller's comic book was not intended to be historically accurate. I believe it was meant to be cool. I know that a lot of people will say that this is bad, because it makes people learn wrong history. Really? Well, in my case, it was pretty obvious that the film was a kind of fiction, unless you really believe that the Persian soldiers were inhuman monsters and that a Spartan soldier can put a spear in the eyes of a giant battle Rhino who is charging on him killing the beast just centimeters before it reaches the target. Of course it was not real! So, the first thing I did when I arrived home was to open a History book and learn what was really known about the fact. See? Although I have never been good in history on my school days, I was led to study it by seeing a movie that made me feel well. If I would have left the cinema feeling that I have thrown my money away, I would never have done that.
In fact, one of the things that led me to be a scientist (and I bet it is the same for many others!) was the Sci-Fi movies. I wanted to live that and, above all, to understand that. Indeed, I almost gave up to be a physicist and just came back after seeing Contact, but this is another story.
Picture: cover of the comic book.
Friday, 30 March 2007
Grand Illusions

The picture above, for those who doesn't know, is a Klein bottle. It is the version of the Mobius strip in one more dimension. The surface has just one side and is non-orientable. This comes from a very interesting site I found one day when I was looking for something completely different in the Internet. Usually this is the way I find the most interesting sites. The site is:
Grand Illusions
It has 4 sections:
1. Toy Shop: in this section they sell a lot of interesting toys. Most, let's say, scientifically inclined. They are a little expensive, but they seem to be very well crafted. They have movies so you can see the toys in action. The Klein bottle of the picture can be purchased there.
2. Toy Collection: more interesting toys and objects, but they are not for sellling.
3. Optical Illusions: a collection of videos and pictures together with explanations. The interesting thing here is that they do not only restrict theirselves to the illusions already known by everyone, there are some modern ones as well.
4. Articles: brief articles about interesting stuff related to the other four sections.
I guess that it is worth to browse the website. I found it quite delighful.
It has 4 sections:
1. Toy Shop: in this section they sell a lot of interesting toys. Most, let's say, scientifically inclined. They are a little expensive, but they seem to be very well crafted. They have movies so you can see the toys in action. The Klein bottle of the picture can be purchased there.
2. Toy Collection: more interesting toys and objects, but they are not for sellling.
3. Optical Illusions: a collection of videos and pictures together with explanations. The interesting thing here is that they do not only restrict theirselves to the illusions already known by everyone, there are some modern ones as well.
4. Articles: brief articles about interesting stuff related to the other four sections.
I guess that it is worth to browse the website. I found it quite delighful.
Thursday, 29 March 2007
Science Maps
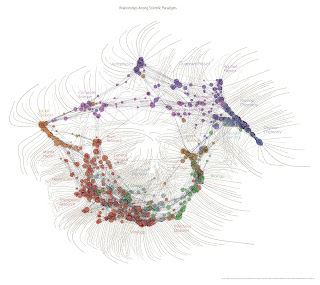
Well, I'm a little pissed off today because me and my wife discovered that, although I am one year out of Brazil, we will have to pay the income tax there as well as here. Yes, we can deduct what we paid here, but here I am also paying the National Health System and a pension scheme, which I cannot deduce. Not a good week...
Well, let us come back to the science world. I was browsing the emails sent by one of my friends as he always send me interesting things and stumbled with the picture above and this link:
Scientific Method: Relationships Among Scientific Paradigms
It is a map relating branches of science whose credits go to Kevin Boyack, Dick Klavans and W. Bradford Paley. The idea is that each area of science, which they call a 'paradigm' and is represented by a circle, shares a link with another area if there is a scientific paper citing both together. I was examining the picture. It is a very beautiful one! But I noted an absence of direct links between the biology branches and physics. I guess that if you read some of my old posts, you know that in Statistical Physics there is a lot of papers relating such areas. For example, I would consider that at least some papers about Neural Networks can be considered related to Brain Research. There are also a lot of papers about the spread of diseases or the working of the immune system in Statistical Physics, which would add some direct links from the bottom to the top of the picture. In a not-so-humble move, I emailed one of the authors today talking about that and suggesting to add a separate circle for Statistical Physics. Come on, I agree it is a biased opinion, but I think that Statistical Physics deserves it.
I also find this page of the project Places & Spaces: Mapping Science, which is an exhibition of similar maps of all kinds of science studies which is touring the world. There are very nice and interesting pictures there and, for those who live here in UK like me, they may come to London and Oxford although the dates are not confirmed.
-------------------
I'm very pleased that Kevin Boyack answered my email so quickly. He explains the question I raised about Statistical Physics and his explanation helps in the understanding of the map:
1. The map is constructed by the most co-cited references, not the most recent ones. Therefore, it is natural that some more recent kinds of work are not present. Just the most refered to.
2. If Statistical Physics appears in these papers in a very interdisciplinary way, it would be spread out in the map and would not be easy to localize. But, as I said, if SP papers are not so cited as others, they will appear less.
3. The algorithm used to constructed the map only draws the strongest links to avoid a very crowded and difficult-to-see map. It is not that the links don't exist, they're just not so stronge as the other ones depicted.
Makes perfect sense. I would like to thank the author for such a nice and quick answer. This is really a very beautiful work.
Well, let us come back to the science world. I was browsing the emails sent by one of my friends as he always send me interesting things and stumbled with the picture above and this link:
Scientific Method: Relationships Among Scientific Paradigms
It is a map relating branches of science whose credits go to Kevin Boyack, Dick Klavans and W. Bradford Paley. The idea is that each area of science, which they call a 'paradigm' and is represented by a circle, shares a link with another area if there is a scientific paper citing both together. I was examining the picture. It is a very beautiful one! But I noted an absence of direct links between the biology branches and physics. I guess that if you read some of my old posts, you know that in Statistical Physics there is a lot of papers relating such areas. For example, I would consider that at least some papers about Neural Networks can be considered related to Brain Research. There are also a lot of papers about the spread of diseases or the working of the immune system in Statistical Physics, which would add some direct links from the bottom to the top of the picture. In a not-so-humble move, I emailed one of the authors today talking about that and suggesting to add a separate circle for Statistical Physics. Come on, I agree it is a biased opinion, but I think that Statistical Physics deserves it.
I also find this page of the project Places & Spaces: Mapping Science, which is an exhibition of similar maps of all kinds of science studies which is touring the world. There are very nice and interesting pictures there and, for those who live here in UK like me, they may come to London and Oxford although the dates are not confirmed.
-------------------
I'm very pleased that Kevin Boyack answered my email so quickly. He explains the question I raised about Statistical Physics and his explanation helps in the understanding of the map:
1. The map is constructed by the most co-cited references, not the most recent ones. Therefore, it is natural that some more recent kinds of work are not present. Just the most refered to.
2. If Statistical Physics appears in these papers in a very interdisciplinary way, it would be spread out in the map and would not be easy to localize. But, as I said, if SP papers are not so cited as others, they will appear less.
3. The algorithm used to constructed the map only draws the strongest links to avoid a very crowded and difficult-to-see map. It is not that the links don't exist, they're just not so stronge as the other ones depicted.
Makes perfect sense. I would like to thank the author for such a nice and quick answer. This is really a very beautiful work.
Wednesday, 21 March 2007
Quantization

After three weeks fighting against an horde of evil bacteria which were trying to eat me alive, I finally have some time to write. It looks a little exaggerated, but apart from the word 'evil' and the fact that it may well be a virus, the rest is true.
Okay, back to physics. While I was in home these days I was studying a little of Loop Quantum Gravity. LQG is also called Canonical Quantum Gravity because the idea is to try to quantize gravity without using perturbative methods by a technique called canonical quantization. Now, instead of talking about what is canonical quantization, I would like to go through another path. I would like to talk about the more general procedure named 'quantization'. I decided to write about it because in one of the papers I was reading the author wrote that LQG was based in a well understood quantization procedure. I do not deny that canonical quantization is a well understood method to transform a classical theory in a quantum one mathematically, but this rang a bell in my head because, in the end, the whole thing of 'quantizing' is, in reality, far from being well understood conceptually. Let me explain better.
Quantum Mechanics is believed to be the true fundamental theory of nature. There is little doubt about that given the overwhelming experimental evidence in favor of it. So, the aim is to make all known theories compatible with QM. But nobody really knows what is the real principles of QM. Yes, this is the truth. However, using a lot of analogies, genial insights and mathematical efforts, we were able to make 3 of the 4 forces known in nature compatible with what we know is true in QM. Nowadays, after more than a century of QM, it seems that we are on our way to quantize the last one, namely gravity, using again mathematical analogies. These mathematical analogies are called quantization methods, but they are exactly that: mathematical techniques. We substitute real variables by hermitian operators, real Poisson brackets by commutators, expand the solution of the equations in Fourier series and define creation and annihilation operators but, what is really going on here, nobody truly knows.
The problem is that is quite embarassing for a theory that should be the fundamental one when we have to derive its equations first from the not-so-correct one and then quantizing (modifying following some recipe) it. Conceptually, it would be desirable to start with some quantum mechanical principles, derive the QM equations and, through some limit, recover the classical results. This would be the ideal, but it seems that we are far away from this goal. And maybe that is the reason why gravity is so difficult to quantize and why there are those incovenient infinities in quantum field theory. Probably, when we find the true quantum principles, we will discover that all the quantization methods are thumb rules to go from one limit to another. This is a difficult endeavour and maybe the solution would just appear when we discover new phenomena or maybe when someone have a strikingly new idea. I will risk to say that this would be still even more exciting than even quantizing gravity, for it would change (again) completely our view of nature.
I'll be optimist and hope that I can see it still in my lifetime. There are quite a lot of clever people working on these matters today. There are the Bayesian approaches, the more or less old Bohmian Mechanics, Nelson's QM and a lot of other tentatives, but something is still lacking. I believe that when the answer comes it will be like when you learn relativity: "Why did nobody think about it before? It's so obvious!" I mean, it is that feeling that every piece has fitted together. Well, I'll wait. :)
Picture: Taken from the University of Tokyo's Website.
Okay, back to physics. While I was in home these days I was studying a little of Loop Quantum Gravity. LQG is also called Canonical Quantum Gravity because the idea is to try to quantize gravity without using perturbative methods by a technique called canonical quantization. Now, instead of talking about what is canonical quantization, I would like to go through another path. I would like to talk about the more general procedure named 'quantization'. I decided to write about it because in one of the papers I was reading the author wrote that LQG was based in a well understood quantization procedure. I do not deny that canonical quantization is a well understood method to transform a classical theory in a quantum one mathematically, but this rang a bell in my head because, in the end, the whole thing of 'quantizing' is, in reality, far from being well understood conceptually. Let me explain better.
Quantum Mechanics is believed to be the true fundamental theory of nature. There is little doubt about that given the overwhelming experimental evidence in favor of it. So, the aim is to make all known theories compatible with QM. But nobody really knows what is the real principles of QM. Yes, this is the truth. However, using a lot of analogies, genial insights and mathematical efforts, we were able to make 3 of the 4 forces known in nature compatible with what we know is true in QM. Nowadays, after more than a century of QM, it seems that we are on our way to quantize the last one, namely gravity, using again mathematical analogies. These mathematical analogies are called quantization methods, but they are exactly that: mathematical techniques. We substitute real variables by hermitian operators, real Poisson brackets by commutators, expand the solution of the equations in Fourier series and define creation and annihilation operators but, what is really going on here, nobody truly knows.
The problem is that is quite embarassing for a theory that should be the fundamental one when we have to derive its equations first from the not-so-correct one and then quantizing (modifying following some recipe) it. Conceptually, it would be desirable to start with some quantum mechanical principles, derive the QM equations and, through some limit, recover the classical results. This would be the ideal, but it seems that we are far away from this goal. And maybe that is the reason why gravity is so difficult to quantize and why there are those incovenient infinities in quantum field theory. Probably, when we find the true quantum principles, we will discover that all the quantization methods are thumb rules to go from one limit to another. This is a difficult endeavour and maybe the solution would just appear when we discover new phenomena or maybe when someone have a strikingly new idea. I will risk to say that this would be still even more exciting than even quantizing gravity, for it would change (again) completely our view of nature.
I'll be optimist and hope that I can see it still in my lifetime. There are quite a lot of clever people working on these matters today. There are the Bayesian approaches, the more or less old Bohmian Mechanics, Nelson's QM and a lot of other tentatives, but something is still lacking. I believe that when the answer comes it will be like when you learn relativity: "Why did nobody think about it before? It's so obvious!" I mean, it is that feeling that every piece has fitted together. Well, I'll wait. :)
Picture: Taken from the University of Tokyo's Website.
Tuesday, 20 February 2007
What's in a name?

See the titles of these papers that I found in this thread on PhysicsForums and decide yourself:
Would Bohr be born if Bohm were born before Born?
H. Nikolic
physics/0702069
IIB or not IIB
Mark Srednicki
hep-th/9807138
If anyone knows papers with interesting names, please feel free to say it.
-------------------
I'm adding two more. One, Osame pointed me (as you can see in the comments), the other I was browsing some papers I collected some time ago and stumbled with it. I guess both can be considered in the same class of the second one above, let us say, Shakespearean Titles:
What's in a name?
Luciano da Fontoura Costa
cond-mat/0309266
Much Ado About Nothing
Vijay Balasubramanian, Klaus Larjo, Joan Simon
hep-th/0502111
Picture: Romeo and Juliet, by Soul-Daemon.
Would Bohr be born if Bohm were born before Born?
H. Nikolic
physics/0702069
IIB or not IIB
Mark Srednicki
hep-th/9807138
If anyone knows papers with interesting names, please feel free to say it.
-------------------
I'm adding two more. One, Osame pointed me (as you can see in the comments), the other I was browsing some papers I collected some time ago and stumbled with it. I guess both can be considered in the same class of the second one above, let us say, Shakespearean Titles:
What's in a name?
Luciano da Fontoura Costa
cond-mat/0309266
Much Ado About Nothing
Vijay Balasubramanian, Klaus Larjo, Joan Simon
hep-th/0502111
Picture: Romeo and Juliet, by Soul-Daemon.
Friday, 16 February 2007
Quantum Computers... so fast?

Last edition: 20/02/2007. I'm adding some links to the scientific terms.
---
Nobody (I mean, physicists) was expecting a commercial quantum computer so fast, but the firm D-Wave, founded by physicist Geordie Rose (who has his own blog) in 1999, claims that achieved just that.
Risking being repetitive, quantum computation becomes an attractive endeavour after P.W. Shor demonstrated in his paper Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer. As prime factorization is a key element in todays public key cryptographic schemes because it is an NP problem for classical computers, i.e. the time necessary to factorize a prime number scales exponentially with the size of the number, a polynomial time algorithm, turning it into what is called a P problem, means a break down of our current electronic security.
Now, quantum computers are very elusive and that's because they relie on entanglement of quantum systems to make the miracle of transforming an NP problem into a P problem. More detailed explanations can be found in the book Quantum Computation and Information or in some sites in the internet:
The Quantum Computer, An Introduction by Jacob West
Lectures on Quantum Computers by David Deutsch
Quantum Computation. Mini-Course, by André Berthiaume
It is difficulty, although, to keep entanglement for a sufficient time to do any useful calculation, for entanglement is quickly lost as it is impossible to avoid interactions with the environment which causes entanglement to fade. D-Wave has just claimed it was successful in doing this for 16 qubits, which is a quantity of information that is already interesting.
Most of physicists, including me, are skeptical about that because D-Wave haven't released to much information about how the computer works and, as groups around the world have been trying it with a lot of different techniques without great results until now, it is surprising that they've achieved it so fast. Anyway, it would really be something exciting if they do that. Let us wait.
While you wait, a press release on PhysicsWeb
Firm claims first "commercial" quantum computer
and a YouTube video of D-Wave's presentation
Picture: taken from The Economist.
PS: I intend to edit this post a little more, adding some links, but I don't have too much time today and I'll do that during the next days.
Tuesday, 13 February 2007
Ferrofluid Video

As written in the Wikipedia:
"A ferrofluid is a liquid that becomes strongly polarised in the presence of a magnetic field. Ferrofluids are composed of nanoscale ferromagnetic particles suspended in a carrier fluid, usually an organic solvent or water."
This is a nice video I found in YouTube showing experiments dealing with shape manipulation of a ferrofluid by a magnetic field. Very beautiful. If you cannot see the image link below, just click here.
"A ferrofluid is a liquid that becomes strongly polarised in the presence of a magnetic field. Ferrofluids are composed of nanoscale ferromagnetic particles suspended in a carrier fluid, usually an organic solvent or water."
This is a nice video I found in YouTube showing experiments dealing with shape manipulation of a ferrofluid by a magnetic field. Very beautiful. If you cannot see the image link below, just click here.
Picture: taken from the Ferrofluid entry on Wikipedia linked in the text above.
Monday, 12 February 2007
Darwin's Day

Today is Darwin's Day. He was born in this day in the year of 1809 and published The Origin of Species in 1859.
Picture: taken from Wikipedia's link to Charles Darwin.
Tuesday, 16 January 2007
I'm back...

First thing: this blog is not dead. I've been working too much and still have not time to post regularly, but I like this sovery much and have no intention of stop writing it.
Although my blog is visited much more when I don't write anything, I'm stubborn enough to continue writing, but I'm taking off the "Hard Bloggin' Scientist" badge from my page once I believe I do not deserve it anymore.
Well, today I'm just posting the comic strip I received from a friend (and which is in the wall of my office now :), not the friend, the strip...) and was taken from an interesting webcomic page: named xkcd.
My future posts, at least for some time, probably will be like this: videos, links and pictures. I hope I have some time to discuss something deeper, but I cannot see it in the near future. Anyway, it is good to be back.
Although my blog is visited much more when I don't write anything, I'm stubborn enough to continue writing, but I'm taking off the "Hard Bloggin' Scientist" badge from my page once I believe I do not deserve it anymore.
Well, today I'm just posting the comic strip I received from a friend (and which is in the wall of my office now :), not the friend, the strip...) and was taken from an interesting webcomic page: named xkcd.
My future posts, at least for some time, probably will be like this: videos, links and pictures. I hope I have some time to discuss something deeper, but I cannot see it in the near future. Anyway, it is good to be back.
Subscribe to:
Posts (Atom)